A Computational Spirit to Learning Mathematics

“A mathematician, like a painter or poet, is a maker of patterns. If his patterns are more permanent than theirs, it is because they are made with ideas.” -- G.H. Hardy

Ever watched a student’s face light up when a piece of mathematics clicks? Not just the dim recognition of memorized formulas nor the blind following of steps, but the deeper personal understanding that comes from making that unexpected link or applying it meaningfully in their own way.

My cofounder and I have been on a quest to help students achieve that satisfying level of understanding by building a shared computational world for students to interact within.

When we let students wrestle with explorable mathematical problems, we noticed they are naturally attracted to patterns and easily stumble into inquiry.

They instinctively seek patterns in the properties of the objects they’re manipulating, whether they’re exploring polygons in a geometric space or playing with number sequences.

They develop their own operations and procedures, sometimes rediscovering classical algorithms, sometimes creating novel approaches that surprise even us.

They invent their own representations to communicate their ideas, from hastily sketched diagrams to improvised pseudo code.

And perhaps most remarkably, they begin to abstract and generalize from their concrete experiences, building bridges across different mathematical territories they’ve explored and have firmer footing on.

Reimagining Learning Mathematics

If these natural processes of mathematical thinking sounds familiar it is only because students are inadvertently navigating the 4 fundamental themes of mathematics set out by MOE:

Mathematical objects and concepts, and related knowledge and methods, are products of insight, logical reasoning and creative thinking, and are often inspired by problems that seek solutions.

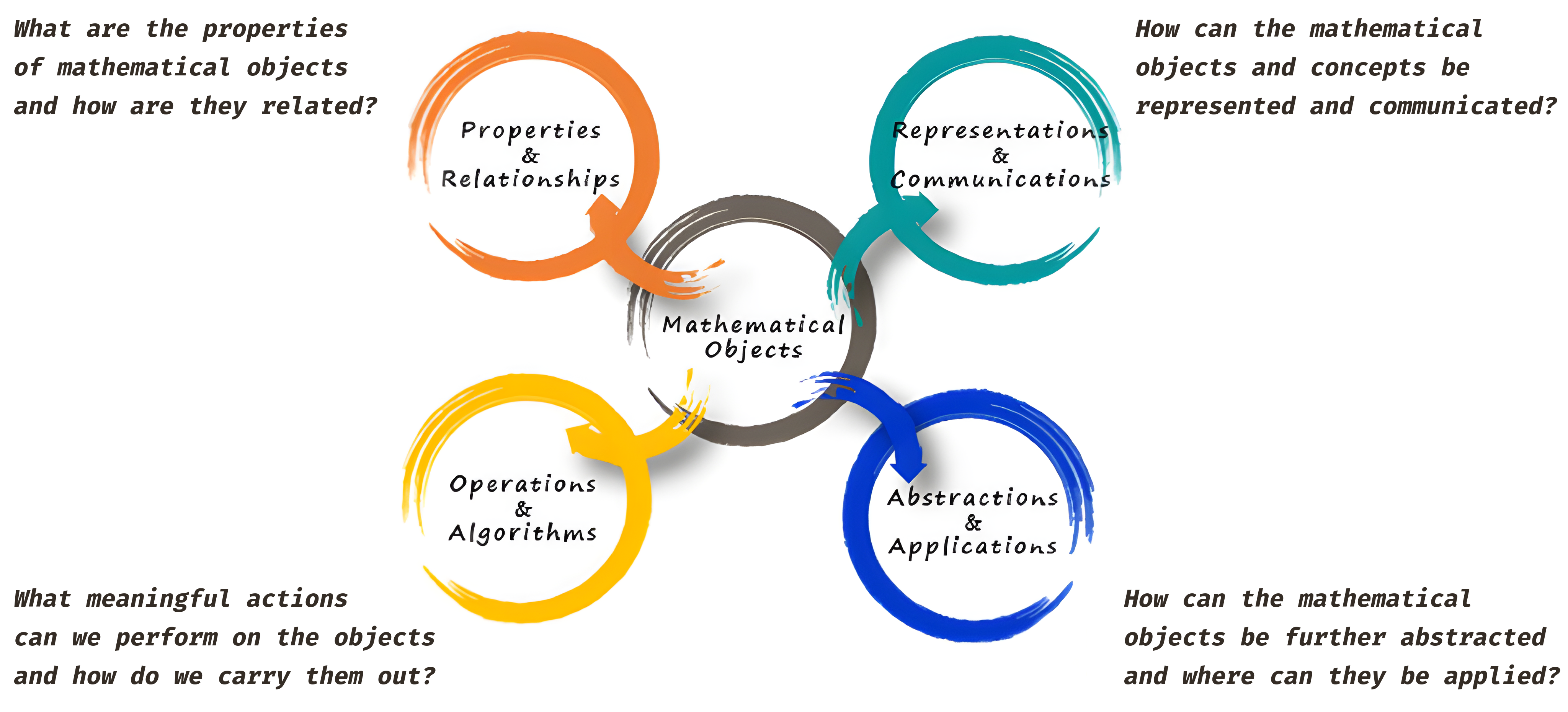
1. Properties and Relationships: What are the properties of mathematical objects and how are they related?
2. Operations and Algorithms: What meaningful actions can we perform on these mathematical objects and how do we carry them out?
3. Abstractions and Applications: How can the mathematical objects be further abstracted and where can they be applied?
4. Representations and Communications: How can these mathematical objects and concepts be represented and communicated?

What’s exciting about the computational learning approach we have been crafting is how it creates an environment where these mathematical instincts can be naturally engaged.

1. Properties & Relationships: Not Fixed but Malleable

⊕ Properties and relationships are not fixed truths to be memorized. Our computational approach transforms these into concepts that students can discover through exploration. By writing and manipulating code, students don’t just learn that polygons have certain properties such as exterior sum of angles – they experience why these properties emerge, pose mini-conjectures, and test their validity through their own investigations.

2. Operations & Algorithms: Process for Discovery

⊕ Algorithms are not mere procedures to be followed and applied. Our approach reveals them as powerful tools for discovery. Students don’t just apply mathematical operations – they build them, understand them, and even improve them. Through computation, the black box of mathematical procedures becomes transparent and interactive, where students can experiment and iterate with immediate feedback.

3. Representations & Communication: Shared Understanding Together

⊕ Mathematical ideas have always lived as symbols, diagrams, and graphs. Our computational platform enriches these by making representations dynamic and interactive. Students can arrive at similar big ideas from their own perspective, and in our multiplayer world, they can copy, collide, and reason against their classmates’ approaches. In code, copying is not a bad word – it’s a stepping stone to understanding and making the code their own - a process that learners can run, modify, and observe.

4. Abstractions & Applications: Building Personal Ladders

⊕ Mathematics has always been about finding patterns and making generalizations. Our computational approach makes this process explicit and accessible. Students don’t just learn about abstractions – they create them, test them, and extend them. Through coding, the leap from concrete instances to underlying abstract principles becomes a more natural journey of taking steps up their own ladders through code and experimentation.

Active Creation

We believe that true mathematical understanding comes not from passive reception but from active creation. By bringing the computational approach into mathematics education, the process of engaging with mathematical ideas begins in a place of inquiry. We are creating an environment where students can:

pose their own subproblems;

play with their own mini-conjectures and discoveries;

take unexpected turns and learn from them;

experience creative frustration;

have moments of inspiration;

question their own assumptions;

debug what’s missing;

and form their own arguments in their own words – ones they’re proud to talk about and share.

This approach is not without its challenges. Like any worthwhile endeavor, it requires patience, guidance, and a willingness to embrace productive confusion. However, it’s only in allowing learners to wrestle with problems that they can form familiarity and put a name to the abstract solutions that arise from them.

Mathematics and the development of its ideas represents the high-water mark of human ingenuity, logical reasoning, the creative discovery of unexpected connections and underlying unity across diverse chapters of human knowledge. Should it not be learned in the same spirit of wholeness?